Question

I need help!

Screenshot down below.
Please give me real answers and not spam (those who spam will get reported)
Please SHOW your work

The formula for the question below is A=Pe^rt

Answer 1

Answer: 23 years

=======================================================

Work Shown:

P = 1000 is the amount deposited

We want this value to double to A = 2000 which is the amount in the account at time t (in years).

r = 0.03 represents the interest rate in decimal form.

The value of t is unknown but we can solve for it like so

`A = Pe^(rt)\\\\2000 = 1000e^(0.03t)\\\\2 = e^(0.03t)\\\\\ln(2) = \ln\left(e^(0.03t)\right)\\\\\ln(2) = 0.03t\ln\left(e\right)\\\\\ln(2) = 0.03t*1\\\\\ln(2) = 0.03t\\\\`

`0.03t = \ln(2)\\\\t = (\ln(2))/(0.03)\\\\t \approx 23.1049060186649\\\\t \approx 23\\\\`

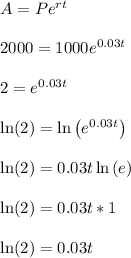
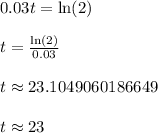
It will take about 23 years for the amount to double.

As a check,

`A = 1000e^(0.03t)\\\\A \approx 1000e^(0.03*23.104906)\\\\A \approx 1,999.9999988806\\\\A \approx 2000\\\\`

which helps show that after roughly 23 years, we'll have about 2000 dollars in the account.

------------

Side note: Use of the rule of 72 leads to 72/3 = 24. The '3' is from the 3% interest rate. So the rule of 72 says it will take about 24 years for the amount to double. This isn't too far off from the 23 answer we got.