Answer:
Approximately
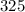 (rounded down,) assuming that
(rounded down,) assuming that
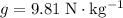 .
.
The number of repetitions would increase if efficiency increases.
Step-by-step explanation:
Ensure that all quantities involved are in standard units:
Energy from the cookie (should be in joules,
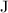 ):
):
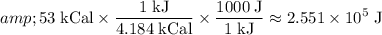 .
.
Height of the weight (should be in meters,
 ):
):
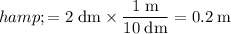 .
.
Energy required to lift the weight by
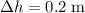 without acceleration:
without acceleration:
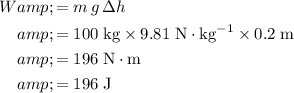 .
.
At an efficiency of
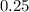 , the actual amount of energy required to raise this weight to that height would be:
, the actual amount of energy required to raise this weight to that height would be:
![\begin{aligned} \text{Energy Input} &= \frac{\text{Useful Work Output}}{\text{Efficiency}} \\ &= \frac{196\; {\rm J}}{0.25} \\ &=784\; {\rm J}\end{aligned}]() .
.
Divide
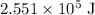 by
by
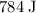 to find the number of times this weight could be lifted up within that energy budget:
to find the number of times this weight could be lifted up within that energy budget:
 .
.
Increasing the efficiency (the denominator) would reduce the amount of energy input required to achieve the same amount of useful work. Thus, the same energy budget would allow this weight to be lifted up for more times.