The correct solution is
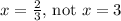 . The error in the solution was in incorrectly setting up the equation to equate the lengths of the segments.
. The error in the solution was in incorrectly setting up the equation to equate the lengths of the segments.
Let's analyze the given solution and identify the error:
1. 4x + 6 = 3x + 9 (Equation representing the segment XY and WZ)
2. x + 6 = 9 (Subtracting 3x from both sides)
3. x = 3 (Subtracting 6 from both sides)
Now, let's check this solution in the context of the given problem:
The equation 4x + 6 = 3x + 9 is an attempt to equate the lengths of XY and WZ. However, it's incorrect because these two segments are not necessarily equal. Instead, the correct equation should be:
XY + YW = WZ
So, the correct equation is:
(4x + 6) + (5x - 1) = 3x + 9
Now, solve for x:
9x + 5 = 3x + 9
Subtract 3x from both sides:
6x + 5 = 9
Subtract 5 from both sides:
6x = 4
Divide by 6:
![\[ x = (2)/(3) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/elr1ndlm0t3b923cvyme3dn0xg3kufonh3.png)
Therefore, the correct solution is
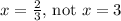 . The error in the solution was in incorrectly setting up the equation to equate the lengths of the segments.
. The error in the solution was in incorrectly setting up the equation to equate the lengths of the segments.