Solve this radical equation:

Question

asked Apr 21, 2021 144k views

2 Answers

Pollirrata · Answer 1 · 2021-04-22T07:05:11+0000

Explanation:

Given,

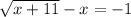
√(x + 11) - x = - 1

To Find:

Solution:

Square both sides, then solve.

$\rm \implies \: \: √((x + 11) ) {}^(2) = ( - 1 + x) {}^(2)$

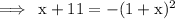
$\implies \rm \: x + 11 = - (1 + x) {}^(2)$

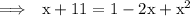
$\rm \implies \: \: x + 11 = 1 - 2x + x {}^(2)$

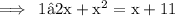
$\rm \implies \: 1−2x+x {}^(2)=x+11$

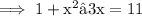
$\rm \implies1+x {}^(2) −3x=11$

$\rm \implies1+x {}^(2) −3x−11=0$

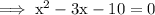
$\rm \implies {x}^(2) - 3x - 10 = 0$

Factor the LHS

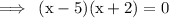
$\implies \rm \: (x - 5)(x + 2) = 0$

Bring terms equal to 0, that is

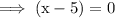
$\implies \rm(x - 5) = 0$

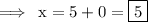
$\implies \rm \: x = 5+ 0 = \boxed 5$

AND set x+2 equal to 0,

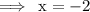
$\rm\implies \: x + 2 = 0$

$\rm \implies \: x = - 2$

So the possible two values are 5 & -2.

But, after plugging the values for verifying each,the most accurate is 5.

So, the value of x is 5.