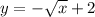Answer:
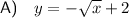
Explanation:
Parent function:
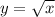
The properties of the parent function are:
- Starts at the origin, so y-intercept is at (0, 0)
- Domain: x ≥ 0
- Range: y ≥ 0
- As x increases, y increases
From inspection of the graph, as the x-values increase, the y-values decrease. Therefore there has been a reflection in the x-axis.
The y-intercept is now at (0, 2), therefore the function has been translated 2 units up.
Translations
For a > 0
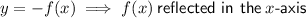
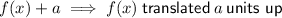
Therefore:
Reflected in the x-axis:
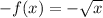
Then translated 2 units up:
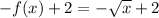
So the equation that represents the transformed function is: