Question

Drag each sign or value to the correct location on the equation. Each sign or value can be used more than once, but not all signs and values will be used.

The focus of a parabola is (-10, -7), and its directrix is x = 16. Fill in the missing terms and signs in the parabola's equation in standard form.

Answer 1

(y+7)^2= -52(x-3)

Explanation:

answer for plato

hope this help Don't forget to like :)

Answer 2

The equation of the parabola in standard form is x = y²/52 + 7·y/26 -
`2(3)/(52)`

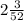
Explanation:

The standard form of a parabola is a·y² + b·y + c

The focus of the parabola = (-10, -7), the directrix is x = 16, we have;

The coordinate of the focus is given as_F(h + p, k)

Where;

p = 1/(4·a)

The equation of the directrix is x = h - p

Therefore, given that the coordinates of the focus = (-10, -7), we have;

k = -7

Given that the equation of the directrix is x = 16, we have;

h - p = 16...(1)

h + p = -10...(2)

Adding equation (1) and (2), gives;

2·h = 6

h = 6/2 = 3

h = 3

From equation (1), p = h - 16 = 3 - 16 = -13

The general equation of the parabola is (y - k)² = 4·p·(x - h), therefore, substituting the values gives;

(y - (-7))² = 4 × (-13) × (x - 3)

(y + 7)² = -52·(x - 3)

y² + 14·y + 49 = -52·x + 156

x = (y² + 14·y + 49 - 156)/(-52) = (y² + 14·y + 49 - 156)/(-52) = y²/52 + 7·y/26 -107/52