Question

at constant pressure by what fraction of its volume will aquantity of gas change if the temperature changes from -173degree C to 27degree C

Answer 1

The volume of the gas becomes three times the initial volume.

Step-by-step explanation:

Given that the pressure is constant, and temperature changes from -173degree C to 27degree C.

So, the initial temperature,
`T_1` = -173 degree C = -173+273 = 100 K.

The final temperature,
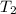`T_2`= 27 degree C = 27+273=300 K.

As the pressure is constant, so
`P_1=P_2`.

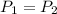Let V_1 and V_2 be the initial and final volume respectively.

Assuming that the given gas is ideal gas.

So, applying the ideal gas equation

PV=nRT

where n is the number of moles of the gas and R is the universal gas constant.

For the initial state,
`P_1V_1=n_1RT_1\cdots(i)`

and for the final state,
`P_2V_2=n_2RT_2 \cdots(ii)`

Dividing the equation (i) by (ii), we have

`\frac {P_1V_1}{P_2V_2}=\frac {n_1RT_1}{n_2RT_2} \\\\\frac {P_1V_1}{P_2V_2}=\frac {n_1T_1}{n_2T_2}`

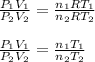
As the mass of the gas is not changing, so
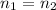`n_1=n_2`, then

`\frac {P_1V_1}{P_2V_2}=\frac {T_1}{T_2}`

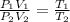
As the pressure is not changing, so
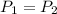`P_1=P_2`, then

`\frac {V_1}{V_2}=\frac {100}{300}`

`V_2=3V_1`

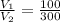
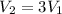
So, the volume of the gas becomes three times the initial volume.