Answer:
They have the same slope
Explanation:
Given
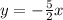
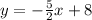
Required
Determine the true statement about both lines
An equation has a general format of:
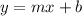
Where
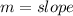
By comparing this to the equations of both lines, we have that:
For line 1:
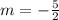
For line 2:
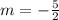
Compare the slopes of both lines, we have that:
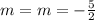
Hence, we can conclude that both lines have the same slope