1.
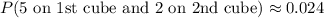
2. A.
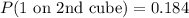
B.
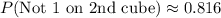
3.

The experimental probability of double sixes is lower than expected, likely due to the limited number of trials.
1. Experimental Probability of Rolling a 5 on the First Cube and a 2 on the Second Cube:
Count the number of times the event occurs and divide it by the total number of trials.
![\[ P(5 \text{ on 1st cube and 2 on 2nd cube}) = (6)/(250) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/yofowx0xxmnfr1z63xovuvpv6y7fpwzq18.png)
![\[ P(5 \text{ on 1st cube and 2 on 2nd cube}) \approx 0.024 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/yul6sh4me3g134a50vs7mbmn94xxld8813.png)
2. A. Experimental Probability of Rolling a 1 on the Second Cube:
![\[ P(1 \text{ on 2nd cube}) = (7 + 8 + 11 + 6 + 9 + 5)/(250) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/xslbzgujzgd8tkqifzx5hb6z9f0yrkcdbl.png)
![\[ P(1 \text{ on 2nd cube}) = (46)/(250) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/u6m58tzcfydmn0gzduz6ncc4vkfrq9bodw.png)
![\[ P(1 \text{ on 2nd cube}) = 0.184 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/3n5zvkuh8de3y6cbgjrgtgdxfuqiwfmpf7.png)
B. Experimental Probability of NOT Rolling a 1 on the Second Cube:
Since there are 6 possible outcomes on a number cube, the complement of rolling a 1 is rolling any other number.
![\[ P(\text{Not 1 on 2nd cube}) = 1 - P(1 \text{ on 2nd cube}) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/lytshp3cbb8uvh7wzfyuvjheul9mnxnv2n.png)
![\[ P(\text{Not 1 on 2nd cube}) = 1 - 0.184 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ok977pjuqpmjhp5gsgnlvoiaqb83w40x97.png)
![\[ P(\text{Not 1 on 2nd cube}) \approx 0.816 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/67c98xepwvpjhl705yefyu4wpx96fmwtkp.png)
3. Experimental Probability of Rolling Double Sixes:
![\[ P(\text{Double Sixes}) = (26)/(250) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/t80b08m493nxp6t8c1d1c44esh5hwiregk.png)
![\[ P(\text{Double Sixes}) = 0.104 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/k8pse1e1ofpqemiesynz4npmc0920pjqw0.png)
Reasoning:
This experimental probability is lower than the theoretical probability (1/36) of rolling double sixes with two fair six-sided dice. The observed frequency might be influenced by the limited number of trials (250), and in a larger sample size, the experimental probability is likely to approach the theoretical probability.