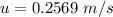Question

A 0.750 kg block is attached to a spring with spring constant 17.5 N/m. While the block is sitting at rest, a student hits it with a hammer and almost instantaneously gives it a speed of 39.0 cm/scm/s . What are:

a. The amplitude of the subsequent oscillations?
b. The block's speed at the point where x= 0.750 A?

Answer 1

a

`A = 0.081 \ m`

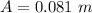
b

The value is
`u = 0.2569 \ m/s`

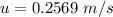
Step-by-step explanation:

From the question we are told that

The mass is
`m = 0.750 \ kg`

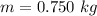
The spring constant is
`k = 17.5 \ N/m`

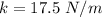
The instantaneous speed is
`v = 39.0 \ cm/s= 0.39 \ m/s`

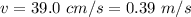
The position consider is x = 0.750A meters from equilibrium point

Generally from the law of energy conservation we have that

The kinetic energy induced by the hammer = The energy stored in the spring

So

`(1)/(2) * m * v^2 = (1)/(2) * k * A^2`

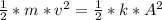
Here a is the amplitude of the subsequent oscillations

=>
`A = \sqrt{(m * v^ 2 )/( k) }`

=>
`A = \sqrt{(0.750 * 0.39 ^ 2 )/(17.5) }`

=>
`A = 0.081 \ m`

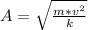
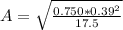
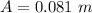
Generally from the law of energy conservation we have that

The kinetic energy by the hammer = The energy stored in the spring at the point considered + The kinetic energy at the considered point

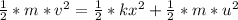
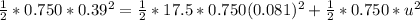
`(1)/(2) * m * v^2 = (1)/(2) * k x^2 + (1)/(2) * m * u^2`

=>
`(1)/(2) * 0.750 * 0.39^2 = (1)/(2) * 17.5* 0.750(0.081 )^2 + (1)/(2) * 0.750 * u^2`

=>
`u = 0.2569 \ m/s`