Question

A recent poll of 1500 new home buyers found that 60% hired a moving company to help them move to their new home. Find the margin of error for this poll if we want 95% confidence in our estimate of the percentage of new home buyers who hired movers.

Answer 1

The margin of error M.O.E = 2.5%

Explanation:

Given that;

The sample size = 1500

The sample proportion
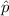`\hat p` = 0.60

Confidencce interval = 0.95

The level of significance ∝ = 1 - C.I

= 1 - 0.95

= 0.05

The critical value:

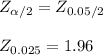`Z_(\alpha/2) = Z_(0.05/2) \\ \\ Z_(0.025) = 1.96` (From the z tables)

The margin of error is calculated by using the formula:

`M.O.E = Z_(\alpha/2) * \sqrt{(\hat p(1 -\hat p))/(n)}`

`M.O.E = 1.96 * \sqrt{(\hat 0.60(1 -0.60))/(1500)}`

`M.O.E = 1.96 * \sqrt{(0.24)/(1500)}`

`M.O.E = 1.96 * \sqrt{1.6 * 10^(-4)}`

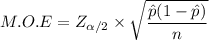
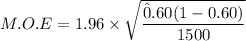
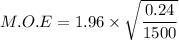
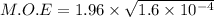
M.O.E = 0.02479

M.O.E ≅ 0.025

The margin of error M.O.E = 2.5%