Question

Kim and Danielle each improved their yards by planting hostas and ivy. They bought their supplies from the same store. Kim spent $62 on 5 hostas and 4 pots of ivy. Danielle spent $144 on 8 hostas and 12 pots of ivy. What is the cost of one hosta?

Answer 1

The cost of one hosta is $6

Explanation:

A system of linear equations is a set of two or more equations of the first degree, in which two or more unknowns are related.

Solving a system of equations consists of finding the value of each unknown so that all the equations of the system are satisfied.

In this case, the variables are:

• x = price of a hosta .
• y = price of a pot of ivy.

If Kim spent $62 on 5 hostas and 4 pots of ivy, t his is represented by the equation: 5*x +4*y= 62

If Danielle spent $144 on 8 hostas and 12 pots of ivy, t his is represented by the equation: 8*x +12*y=144

So, the system of equations to solve is:

`\left \{ {{5*x+4*y=62} \atop {8*x+12*y=144}} \right.`

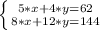
One way to solve a system of equations is through the substitution method, which consists of solving or isolating one of the unknowns (for example, x) and substituting its expression in the other equation. In this way, you obtain an equation of the first degree with the other unknown, and. Once solved, you calculate the value of x by substituting the already known value of y.

Isolating y from the first equation:

`y=(62-5*x)/(4)`

and replacing this expression in the second equation you get:

`8*x +12*(62-5*x)/(4)=144`

Solving:

`8*x +(12)/(4)*(62-5*x)=144`

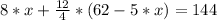
8*x + 3*(62-5*x)=144

8*x + 3*62 - 3*5*x=144

8*x + 186 - 15*x=144

8*x - 15*x=144 -186

(-7)*x= -42

x= (-42)÷ (-7)

x= 6

The cost of one hosta is $6