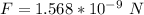Answer:
The value is
Step-by-step explanation:
From the question we are told that
The mass of the first lead sphere is
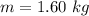
The mass of the second lead sphere is
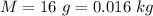
The separation between masses is
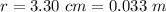
Generally the gravitational force between each sphere is mathematically represented as
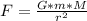
Here G is the gravitational constant with value
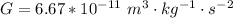
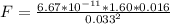
=>