Question

Write a polynomial for the given real-world situation. If the length of a rectangle is 3x^2-4x+5 and the width is 2x + 1, write and simplify a polynomial expression for the area of the rectangle. 3 points for mathematical process and 2 points for correct answer.

Answer 1

`Area = 6x^3+-5x^(2) +6x+5`

Explanation:

Given that:

Length of a rectangle =
`3x^2-4x+5`

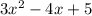
Width of rectangle =
`2x + 1`

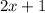
To find:

Simple polynomial expression for finding the area of rectangle.

Solution:

First of all, we should know about the formula for finding the area of rectangle. Then we should know how to multiply two polynomials.

Formula for area of a rectangle in terms of its length and width is:

`Area= Length * Width`

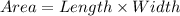
Putting the given values:

`Area = (3x^2-4x+5)(2x+1)`

Here, we can use the distributive property of multiplication for finding the value of the above multiplication expression.

`(A+B)* (C+D) = A* C + A* D+ B* C + B * D`

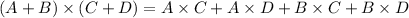
Therefore, the multiplication of above polynomials can be written as:

`Area = (3x^2-4x+5)(2x+1)\\\Rightarrow Area = 3x^2(2x+1)-4x(2x+1)+5(2x+1)\\\Rightarrow Area = 6x^3+3x^(2) -8x^(2) -4x+10x+5\\\Rightarrow Area = 6x^3+-5x^(2) +6x+5`

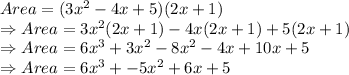
Therefore, the answer is:

`Area = 6x^3+-5x^(2) +6x+5`