Question

Kyle is flying a helicopter at 125 m/s on a heading of 325 o . If a wind is blowing at 25 m/s toward a direction of 240.0 o , what is the craft's resultant velocity?

Answer 1

The resultant velocity of the helicopter is
`\vec v_(H) = \left(89.894\,(m)/(s), -93.348\,(m)/(s)\right)`.

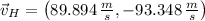Step-by-step explanation:

Physically speaking, the resulting velocity of the helicopter (
`\vec v_(H)`), measured in meters per second, is equal to the absolute velocity of the wind (
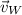`\vec v_(W)`), measured in meters per second, plus the velocity of the helicopter relative to wind (
`\vec v_(H/W)`), also call velocity at still air, measured in meters per second. That is:

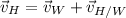`\vec v_(H) = \vec v_(W)+\vec v_(H/W)` (1)

In addition, vectors in rectangular form are defined by the following expression:

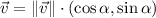`\vec v = \|\vec v\| \cdot (\cos \alpha, \sin \alpha)` (2)

Where:

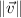`\|\vec v\|` - Magnitude, measured in meters per second.

`\alpha` - Direction angle, measured in sexagesimal degrees.

Then, (1) is expanded by applying (2):

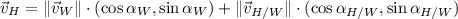`\vec v_(H) = \|\vec v_(W)\| \cdot (\cos \alpha_(W),\sin \alpha_(W)) +\|\vec v_(H/W)\| \cdot (\cos \alpha_(H/W),\sin \alpha_(H/W))` (3)

`\vec v_(H) = \left(\|\vec v_(W)\|\cdot \cos \alpha_(W)+\|\vec v_(H/W)\|\cdot \cos \alpha_(H/W), \|\vec v_(W)\|\cdot \sin \alpha_(W)+\|\vec v_(H/W)\|\cdot \sin \alpha_(H/W) \right)`

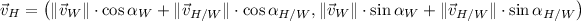
If we know that
`\|\vec v_(W)\| = 25\,(m)/(s)`,
`\|\vec v_(H/W)\| = 125\,(m)/(s)`,
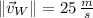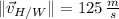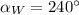`\alpha_(W) = 240^(\circ)` and
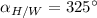`\alpha_(H/W) = 325^(\circ)`, then the resulting velocity of the helicopter is:

`\vec v_(H) = \left(\left(25\,(m)/(s) \right)\cdot \cos 240^(\circ)+\left(125\,(m)/(s) \right)\cdot \cos 325^(\circ), \left(25\,(m)/(s) \right)\cdot \sin 240^(\circ)+\left(125\,(m)/(s) \right)\cdot \sin 325^(\circ)\right)`
`\vec v_(H) = \left(89.894\,(m)/(s), -93.348\,(m)/(s)\right)`

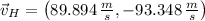
The resultant velocity of the helicopter is
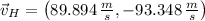`\vec v_(H) = \left(89.894\,(m)/(s), -93.348\,(m)/(s)\right)`.