Question

Considering only (110), (1 1 0), (101), and (10 1 ) as the possible slip planes, calculate the stress at which a BCC single crystal will yield if the critical resolved shear stress is 50 MPa and the load is applied in the [100] direction.

Answer 1

i. Slip plane (1 1 0)

Slip direction -- [1 1 1]

Applied stress direction = ( 1 0 0 ]

τ = 50 MPa ( Here slip direction must be perpendicular to slip plane)

τ = σ cos Φ cos λ

`$\cos \phi = ((1,0,0) \cdot (1,1,0))/(1 * \sqrt2)$`

`$=(1)/(\sqrt2 )$`

`$\cos \lambda = ((1,0,0) \cdot (1,-1,1))/(1 * \sqrt3)$`

`$=(1)/(\sqrt3 )$`

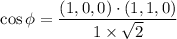
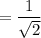
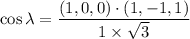
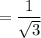
τ = σ cos Φ cos λ

∴
`$50= \sigma * (1)/(\sqrt2) * (1)/(\sqrt3) $`

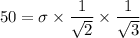
σ = 122.47 MPa

ii. Slip plane --- (1 1 0)

Slip direction -- [1 1 1]

`$\cos \phi = ((1, 0, 0) \cdot (1, -1, 0))/(1 * \sqrt2) =(1)/(\sqrt2)$`

`$\cos \lambda = ((1, 0, 0) \cdot (1, 1, -1))/(1 * \sqrt3) =(1)/(\sqrt3)$`

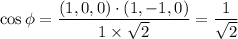
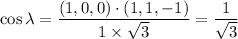
τ = σ cos Φ cos λ

∴
`$50= \sigma * (1)/(\sqrt2) * (1)/(\sqrt3) $`

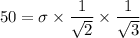
σ = 122.47 MPa

iii. Slip plane --- (1 0 1)

Slip direction --- [1 1 1]

`$\cos \phi = ((1, 0, 0) \cdot (1, 0, 1))/(1 * \sqrt2) =(1)/(\sqrt2)$`

`$\cos \lambda = ((1, 0, 0) \cdot (1, 1, -1))/(1 * \sqrt3) =(1)/(\sqrt3)$`

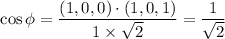
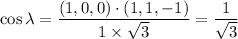
τ = σ cos Φ cos λ

∴
`$50= \sigma * (1)/(\sqrt2) * (1)/(\sqrt3) $`

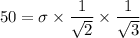
σ = 122.47 MPa

iv. Slip plane -- (1 0 1)

Slip direction ---- [1 1 1]

`$\cos \phi = ((1, 0, 0) \cdot (1, 0, -1))/(1 * \sqrt2)=(1)/(\sqrt2)$`

`$\cos \lambda = ((1, 0, 0) \cdot (1, -1, 1))/(1 * \sqrt3) =(1)/(\sqrt3)$`

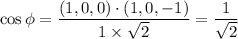
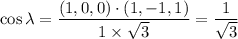
τ = σ cos Φ cos λ

∴
`$50= \sigma * (1)/(\sqrt2) * (1)/(\sqrt3) $`

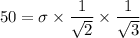
σ = 122.47 MPa

∴ (1, 0, -1). (1, -1, 1) = 1 + 0 - 1 = 0