Question

I am just confused on how to do this question. A 37-inch TV is 37-inches diagonally across the screen. Which of these dimensions best describes a 37-inch TV? A. 15 x 34 B. 16.5 x 32 C. 17 x 28 D. 17 x 32

Answer 1

Given that,

A TV is 27 inch diagonally across the screen.

To find,

The dimensions that best describes a 37 inch TV.

Solution,

Let a and b are length and width of the TV. Let c be the diagonal. Using Pythagoras theorem,

`c=√(a^2+b^2)`

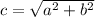
If dimensions are 15 x 34,

`c=\sqrt{15^(2)+34^(2)}\\\\=37.16\ inch`

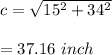
If dimensions are 16.5 x 32,

`c=\sqrt{16.5^(2)+32^(2)}\\\\=36.003\ inch`

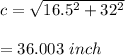
If dimensions are 17 x 28,

`c=\sqrt{17^(2)+28^(2)}\\\\=32.756\ inch`

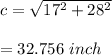
If dimensions are 17 x 32,

`c=\sqrt{17^(2)+32^(2)}\\\\=36.23\ inch`

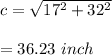
It is clear that if dimensions are 15 x 34, the diagonal is 37 inches. Hence, the correct option is (a).