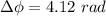Answer:
The value is
Step-by-step explanation:
From the question we are told that
The frequency of each sound is
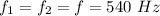
The speed of the sounds is
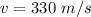
The distance of the first source from the point considered is
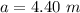
The distance of the second source from the point considered is
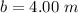
Generally the phase angle made by the first sound wave at the considered point is mathematically represented as
![\phi_a = 2 \pi [(a)/(\lambda) + ft]](https://img.qammunity.org/2021/formulas/physics/high-school/cn1uho2x68oqkyuft7hz0q3rq9r9ym4iao.png)
Generally the phase angle made by the first sound wave at the considered point is mathematically represented as
![\phi_b = 2 \pi [(b)/(\lambda) + ft]](https://img.qammunity.org/2021/formulas/physics/high-school/nyi9b24re7g63f6gi2x4fcptqil2v342s0.png)
Here b is the distance o f the first wave from the considered point
Gnerally the phase diffencence is mathematically represented as
![\Delta \phi= \phi_a - \phi_b = 2 \pi [( a)/(\lambda) + ft ] - 2 \pi [(b)/(\lambda) + ft ]](https://img.qammunity.org/2021/formulas/physics/high-school/9jom7vwfav1qrs9g1k78tj1aloc1gcm57f.png)
=>
![\Delta \phi = (2\pi [ a - b])/( \lambda )](https://img.qammunity.org/2021/formulas/physics/high-school/7qkreobhhtqx7cty83eguaqms6axjtu528.png)
Gnerally the wavelength is mathematically represented as
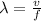
=>
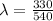
=>
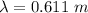
=>
![\Delta \phi = (2* 3.142 [ 4.40 - 4.0 ])/( 0.611 )](https://img.qammunity.org/2021/formulas/physics/high-school/pmzi7ij3dv6y26k0zdxjvpbng2eyrxpzvb.png)
=>