Answer:
v₀ = 2.68 m/s.
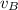 = 3.33 m/s
= 3.33 m/s
d = 1.61 m
Step-by-step explanation:
Searching on the internet I found the picture of the answer in which the height between point A and point B is equal to 0.2 m.
To determine the value of v₀ we need to use the following equation:
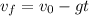
Taking the initial vertical velocity (
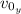 ) as
) as
 and the final vertical velocity (
and the final vertical velocity (
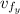 ) as
) as
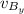 we have:
we have:
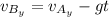
We can express the time (t) in terms of the velocities of A and B:
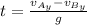 (1)
(1)
Now, we can use the equation:
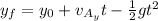 (2)
(2)
By entering equation (1) into equation (2):
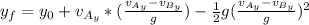 (3)
(3)
Since
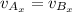 because there is no acceleration in the horizontal movement, we have:
because there is no acceleration in the horizontal movement, we have:
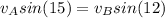
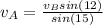 (4)
(4)
Taking:
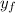 = 0
= 0
 = 0.2 m
= 0.2 m
g = 9.81 m/s²
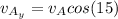
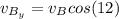
Entering the above values and equation (4) into equation (3) we have:
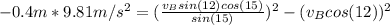
By solving the above quadratic equation:
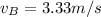
Hence, the velocity of the ball
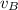 is 3.33 m/s.
is 3.33 m/s.
Now, we can find
 by using equation (4):
by using equation (4):
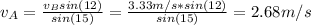
Then, the value of v₀ of the ball is 2.68 m/s.
Finally, to find the distance between point A and point B we need to calculate the time by using equation (1):
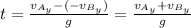
The minus sign in
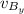 is because the vertical component of the vector is negative.
is because the vertical component of the vector is negative.
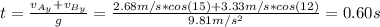
Now, the distance is:
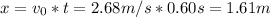
I hope it helps you!