Answer:

A maximum of
 428 miles is the distance what Divya can travel.
428 miles is the distance what Divya can travel.
Explanation:
Given that:
Rent to be paid for the car in the weekend = $200
Charges to be paid per mile = $0.07
Total money available with Divya = $230
To find:
The inequality as per her limitations and solution to the problem.
Solution:
Let the number of miles for which Divya can drive =
 miles
miles
Charges for one mile = $0.07
Charges for
 miles = $0.07
miles = $0.07

Total charges for renting and
 miles = Rental charges + Operational charges
miles = Rental charges + Operational charges
Total charges for renting and
 miles = $200 + $0.07
miles = $200 + $0.07

These are charges must be lesser than equal to the amount of money available with Divya.
Therefore, we can write:

Subtracting 200 from both the sides:
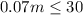
Dividing both sides with 0.07:
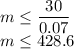
Therefore, a maximum of
 428 miles is the distance what Divya can travel.
428 miles is the distance what Divya can travel.