Answer:
Let x = number of half-page advertisements
Let y = number of full-page advertisements
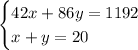
8 full-page advertisements
12 half-page advertisements
Explanation:
Definition of variables
Let x = number of half-page advertisements
Let y = number of full-page advertisements
Given information:
- cost per half-page advertisement = $42
- cost per full-page advertisement = $86
- total budget = $1192
- number of advertisements to purchase = 20
Using the given information, we can write a system of equations:
Equation 1: 42x + 86y = 1192
Equation 2: x + y = 20
To solve the system of equations, rearrange Equation 2 to make x the subject:
⇒ x = 20 - y
then substitute this into Equation 1 and solve for y:
⇒ 42(20 - y) + 86y = 1192
⇒ 840 - 42y + 86y = 1192
⇒ 840 + 44y = 1192
⇒ 44y = 352
⇒ y = 8
Substitute the found value of y into Equation 2 and solve for x:
⇒ x + 8 = 20
⇒ x = 12
Therefore, Kathryn purchased:
- 8 full-page advertisements
- 12 half-page advertisements