Question

One of the Great Pyramids in Egypt has the shape of a square pyramid with the base length of 20 feet, and the height of 150 feet tall. If the stones that were used to build the pyramid had a volume of 40 cubic feet each, how many stones did the Egyptians need to build the pyramid?

Answer 1

500

Explanation:

Given that:

Shape of one of the Great Pyramids in Egypt is a square pyramid.

Base of pyramid is of square shape with length = 20 feet

Height of pyramid = 150 feet

Volume of each stone used for the construction of the pyramid = 40 cubic feet

To find:

Number of stones used for the construction of the pyramid.

Solution:

First, we need to find the volume of the square pyramid and then we need to divide the volume of pyramid with the volume of one stone used for the construction.

It will give us the number of stones used for the construction of pyramid.

Volume of a pyramid is given as:

`V = (1)/(3)* \text{Area of base}* Height`

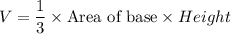
Here, base is a square, so area of base =
`(Side)^2`

`V = (1)/(3)* 20^2* 150 = 400* 50 ft^3`

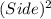
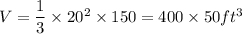
Number of stones of 40 cubic feet each, required =
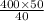`(400* 50)/(40)` = 500