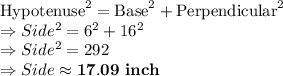Question

If one diagonal is 12 inches long and the other is 32 inches long, how many inches long, to the nearest hundredth of an inch, is a side of the rhombus

Answer 1

17.09 inch

Explanation:

Given that:

A rhombus with diagonals of length 12 inches and 32 inches.

To find:

The length of rhombus to the nearest hundredth of an inch.

Solution:

First of all, we need to learn about the property of a rhombus, its sides and its diagonals.

The diagonals of a rhombus intersect each other by bisecting each other and are perpendicular to each other.

And all the sides

Kindly refer to the attached image for the given dimensions.

Now, there are four right angled triangles in which we can use Pythagorean theorem to find hypotenuse which is nothing but the side of rhombus.

According to Pythagorean theorem:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Perpendicular}^(2)\\\Rightarrow Side^(2) = 6^(2) + 16^(2)\\\Rightarrow Side^(2) = 292\\\Rightarrow Side \approx \bold{17.09\ inch}`