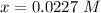Question

What is the molar solubility of nickel(II) sulfide in 0.091 M KCN? For NiS, Ksp = 3.0 × 10 –19; for Ni(CN) 4 2–, Kf = 1.0 × 10 31.

Answer 1

The value is
`x = 0.0227 \ M`

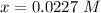
Step-by-step explanation:

From the question we are told that

The concentration of
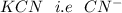`KCN \ \ i.e \ \ CN^(-)` is
`M_1 = 0.091 \ M`

The solubility product constant for
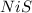`NiS` is
`K_(sp) = 3.0 *10^(-19)`

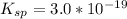
The stability constant for
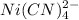`Ni(CN)_4 ^(2-)` is
`K_f = 1.0 *10^(31)`

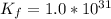
Generally the dissociation reaction for NiS is

`Ni S \underset{}{\stackrel{}{\rightleftharpoons}} Ni^(2+) + S^(2-)`

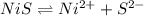
Generally the formation reaction for
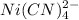`Ni(CN)_4 ^(2-)` is

`4CN^- + N_i ^(2+) \underset{}{\stackrel{}{\rightleftharpoons}} \ Ni(CN)^(2-)_(4)`

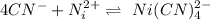
Combining both reaction we have

`4CN^ - + NiS \ \underset{}{\stackrel{}{\rightleftharpoons}} \ Ni(CN)^(2-)_4 + S^(2-)`

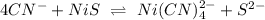
Gnerally the equilibrium constant for this reaction is

`K_c = K_(sp) * K_f`

=>
`K_c = 3.0 *10^(-19 ) * 1.0 *10^(31)`

=>
`K_c = 3.0*10^(12)`

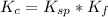
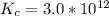
Generally the I C E table for the above reaction is

`4CN^ - \ \ \ + \ \ \ NiS \ \ \ \ \ \ \ \underset{}{\stackrel{}{\rightleftharpoons}} \ \ \ \ \ Ni(CN)^(2-)_4 \ \ \ \ \ \ \ \ \ + \ \ \ \ \ \ \ \ \ S^(2-)`

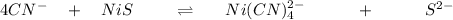
initial [ I] 0.091 0 0

Change [C] -4x +x + x

Equilibrium [E ] 0.091 - 4x x x

Here is x is the amount in term of concentration that is lost by
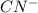`CN^-` and gained by
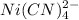`Ni(CN)_4 ^(2-)` and
`S^(2-)`

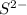
Gnerally the equilibrium constant for this reaction is mathematically represented as

`K_c = ([Ni (CN)_4^(2-) ] [S^(2-) ] )/( [CN^(-)]^4)`

=>
`3.0*10^(12) = (x * x)/( [0.091 - 4x ]^4)`

=>
`3.0*10^(12)* [0.091 - 4x ]^4 = x^2`

=>
`[0.091 - 4x ]^4 = (x^2)/(3.0*10^(12))`

=>
`[0.091 - 4x ] = \sqrt[4]{ (x^2)/(3.0*10^(12))}`

=>
`[0.091 - 4x ] = (√(x) )/(1316)`

=>
`119.8 - 5264x =√(x)`

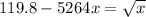
Square both sides

`(119.8 - 5264x)^2 =x`

=>
`14352.04 - 1261255 x + 27709696x^2 = 0`

=>
`27709696x^2 - 1261255 x + 14352.04 = 0`

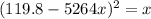
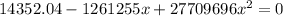
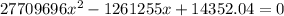
Solving using quadratic equation

The value of x is
`x = 0.0227 \ M`

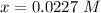
Hence the amount in terms of molarity (concentration) of
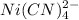`Ni(CN)_4 ^(2-)` and
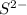`S^(2-)` produced at equilibrium is
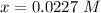`x = 0.0227 \ M` it then means that the amount of NiS (nickel(II) sulfide) lost at equilibrium is
`x = 0.0227 \ M`

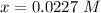
So the molar solubility of nickel(II) sulfide at equilibrium is

`x = 0.0227 \ M`