Answer:
The value is

Step-by-step explanation:
From the question we are told that
The distance of the speaker from the second speaker to the east is
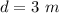
The distance of the speaker from the listener to the south is
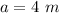
Generally given that if the speaker move in any direction, their sound become louder , it then mean that the position of the listener of minimum sound (i.e a position of minima ) ,
Generally the path difference of the sound produce by both speaker at a position of minima is mathematically represented as
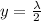
Generally considering the orientation of the speakers and applying Pythagoras theorem we see that distance from the second speaker to the listener is mathematically represented as
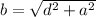
=>
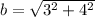
=>
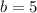
Generally the path difference between the two speaker with respect to the listener is

=>
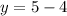
=>
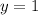
So

=>
