Question

(1 point) Find the size of the sample needed to estimate the difference between the proportions of boys and girls under 10 years old who are afraid of spiders. Assume that we want 9595% confidence that the error is smaller than 0.03.

Answer 1

The size of the sample = 1088.90

Explanation:

Given that:

The confidence interval level = 0.95

The margin of error = 0.03

Suppose the proportion of the boys and the girls are p₁ and p₂ respectively.

The Standard error S.E of difference is:

`S.E (p_1-P_2) = \sqrt{ (p_1(1-p_1) )/(n) + (p_2(1-p_2))/(n) }`

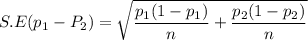
Assume p₁ = p₂ = 0.5

`S.E (p_1-P_2) = \sqrt{ (0.5(1-0.5) )/(n) + (0.5(1-0.5))/(n) }`

`S.E (p_1-P_2) =(0.70711)/(√(n))`

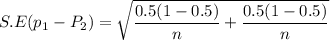
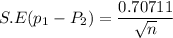
The z-critical value at 95% C.I = 1.96

Margin of error = Z_{critical} × S.E

∴

`0.03 = 1.96 * (0.70711)/(√(n))`

`n =(\left(1.96\ \cdot\ 0.70711^(2)\right))/(0.03^(2))`

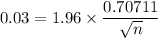
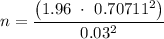
n ≅ 1088.90