Question

A spherical balloon is being deflated at a rate of 5 cubic centimeters per second. At what rate is the radius of the balloon changing at the instant the volume of the balloon 972pi cm^3?

Answer 1

0.0048cm/s

Explanation:

Volume of the spherical balloon is expressed as;

`V = 4/3 \pi r^3\\`

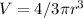
dV/dt = dV/dr * dr/dt

Given

dV/dt = 5cm³/s

dV/dr = 4πr²

Since V = 972picm³

972π = 4/3πr³

972 = 4/3r³

4r³ = 972 * 3

r³ = (972 *3)/4

r³ = 729

r = ∛729

r = 9cm

dV/dr = 4π(9)²

dV/dr = 324π

dV/dt = dV/dr * dr/dt

5 = 324πdr/dt

dr/dt = 5/324π

dr/dt = 5/324(3.14)

dr/dt = 5/1017.36

dr/dt = 0.0048cm/s