Question

I have a cylinder shaped glass container that is 15 cm tall. It holds 100 cm^3 of nitrogen gas at 1 atm pressure (101.3 kPa) and 22 degrees C. I place a rubber stopper in the top so that no gas can escape. If a 40 N force is required to force the rubber stopper off the top of the flask, what temperature can I heat the nitrogen to with a Bunsen burner before the rubber stopper pops off

Answer 1

T₂ = 469.73 K = 196.73 °C

Step-by-step explanation:

First we will find the surface area of rubber stop:

`Area = A= (Volume)/(Length) \\\\A = (100\ cm^3)/(15\ cm)\\\\A = 6.67\ cm^2 = 6.67 \ x\ 10^(-4)\ m^2`

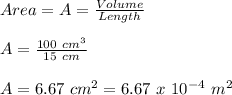
Now, we will find the final pressure required to remove the rubber stop:

`Final\ Pressure\ = P_(2) = (Force)/(Area)+Atmospheric Pressure \\\\P_(2) = (40\ N)/(6.67\ x\ 10^(-4)\ m^2) + 101.3 KPa\\\\ P_(2) = 60000\ Pa + 101.3 KPa = 60\ KPa + 101.3 KPa\\\\P_(2) = 161.3\ KPa`

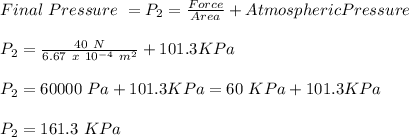
Now, we use equation of state:

`(P_(1) V_(1))/(T_(1)) = (P_(2) V_(2))/(T_(2))`

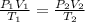
for constant volume due to rigid cylinder:

`(P_(1))/(T_(1)) = (P_(2))/(T_(2))\\\\T_(2) = (P_(2) T_(1))/(P_(1))`

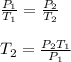
where,

P₁ = initial pressure = 101.3 KPa

P₂ = final pressure = 161.3 KPa

T₁ = Initial Temperature = 22°C = 295 K

T₂ = Final Temperature = ?

Therefore,

`T_(2) = ((161.3\ KPa)(295\ K))/(101.3\ KPa)`

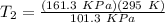
T₂ = 469.73 K = 196.73 °C