Question

Calculate the discriminant and determine the type and number of solutions for each quadratic equation. 2x2−28x=−48 discriminant: Number of solutions: Type of Solutions: Rational or irrational:

Answer 1

Discriminant = 100

Number of solutions = 2

Type of solution = Real and Unique

Rational or Irrational: Rational

Explanation:

Given the quadratic expression;

`2x^2 - 28x= - 48 \\`

Rewrite in standard form

`2x^2 - 28x+ 48= 0 \\`

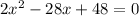
Divide through by 2;

`x^2 - 14x + 24 = 0`

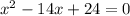
From the expression;

a = 1, b = -14 c = 24

Discriminant determines the nature of the root of the quadratic equation;

Discriminant D = b² - 4ac

Substitute the given values;

D = (-14)² - 4(1)(24)

D = 196 - 96

D = 100

Since the discriminant is greater than zero this means that the solution will be real and unique values.

Get the number of solutions;

Using the formula;

x = -b±√D/2a

x = -(-14)±√100/2(1)

x = 14±10/2

x = 14+10/2 and 14-10/2

x = 24/2 and 4/2

x = 12 and 2

Hence the equation has 2 solutions.

The solutions are rational since we can write then as a ratio of two integers