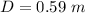Complete Question
Due to blurring caused by atmospheric distortion, the best resolution that can be obtained by a normal, earth-based, visible-light telescope is about 0.3 arcsecond (there are 60 arcminutes in a degree and 60 arcseconds in an arcminute).Using Rayleigh's criterion, calculate the diameter of an earth-based telescope that gives this resolution with 700 nm light
Answer:
The diameter is
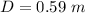
Step-by-step explanation:
From the question we are told that
The best resolution is
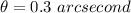
The wavelength is
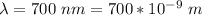
Generally the
1 arcminute = > 60 arcseconds
=> x arcminute => 0.3 arcsecond
So
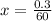
=>
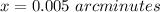
Now
60 arcminutes => 1 degree
0.005 arcminutes = > z degrees
=>
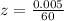
=>
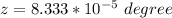
Converting to radian
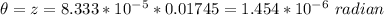
Generally the resolution is mathematically represented as
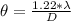
=>

=>
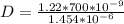
=>