Answer:
E = 8.83 kips
Step-by-step explanation:
First, we determine the stress on the rod:
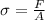
where,
σ = stress = ?
F = Force Applied = 1300 lb
A = Cross-sectional Area of rod = 0.5
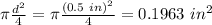
Therefore,
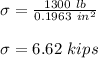
Now, we determine the strain:
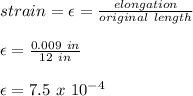
Now, the modulus of elasticity (E) is given as:
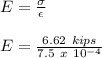
E = 8.83 kips