Question

The mean balance of all checking accounts at a bank on December 31, 2005, was $900. A random sample of 53 checking accounts taken recently from this bank gave a mean balance of $841 with a standard deviation of $190. Using the 1% significance level, can you conclude that the mean balance of such accounts has decreased during this period

Answer 1

Explanation:

Given that:

The population mean μ = 900

The sample size n = 53

The sample mean = 841

The standard deviation = 190

The level of significance = 0.01

To test the claim that the mean balance of the accounts has decreased during the period.

The null and the alternative hypothesis can be computed as:

`H_o : \mu \ge 900 \\ \\ H_1 : \mu < 900`

This is a left-tailed test since the alternative is less than 900

The test statistics can be computed as:

`Z = (\overline x - \mu)/((s)/(√(n)) )`

`Z = (841 -900)/((190)/(√(53)) )`

`Z = (-59)/((190)/(7.28))`

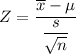
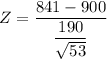
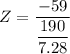
Z = -2.26

The p-value = P(Z < -2.26)

From the z-tables

The p-value = 0.01191

The p-value ≅ 0.012

Decision rule: To reject the null hypothesis if the significance level is > p-value.

We failed to reject the null hypothesis.

Conclusion: Thus, there is insufficient evidence to conclude that such accounts mean balance has decreased during this period.