Question

A hiker travels at 2.8 miles per hour at a heading of N49°W from a ranger station. After 4 hours, how far north and how far west is the hike from the ranger station?

Answer 1

Explanation:

The diagram showing the pictorial view is attached below.

From the image, the distance of the hiker traveled which is denoted by "h" can be determined as follows:

h = 2.8 mi/hr × 4 hr

h = 11.2 mi

Using the trigonometric function;

The distance of how far North is the hike from the ranger station can be determined by using the function of Sin θ

`Sin \theta = (opposite)/(hypotenuse)`

`Sin(41^0) = (x)/(11.2)`

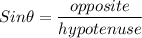
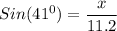
x = Sin 41 (11.2)

x = 0.6561(11.2)

x = 7.34832

x ≅ 7.35 miles

The distance of how far west the hike from the ranger station is calculated by using:

`cos \theta = (adjacent)/(hypotenuse)`

`cos (41^0)= (y)/(11.2)`

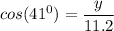
y = 0.7547 × (11.2)

y = 8.45 miles