Question

14. The diagram in Fig. 1.34 shows a uniform metre rule

weighing 100 gf, pivoted at its centre 0. Two weights
150 gf and 250 gf hang from the points A and B
respectively of the metre rule such that OA = 40 cm
and OB = 20 cm. Calculate : (i) the total anticlockwise
moment about O, (ii) the total clockwise moment about
O, (iii) the difference of anticlockwise and clockwise
moments, and (iv) the distance from O where a 100 gf
weight should be placed to balance the metre rule.
7-20 cm
А
승
B
40 cm
)
150 gf
Fig. 1.34
250 gf

Answer 1

(i) The total anticlockwise moment about O, is 6000 + 50 × OD

(ii) The total clockwise moment about O, is 5000 + 50 × OC

(iii) The difference between the anticlockwise and the clockwise moment is 1000 N·cm

(iv) The distance from O where a 100 gf force should be placed to balance the meter rule is 10 cm to the right of the point O on the meter rule

Explanation:

The given parameters are;

The mass of the uniform meter rule = 100 gf

The center of the meter rule = O

The mass of the weight at point A = 150 gf

The mass of the weight at point B = 250 gf

The distance of the point A from the point O = OA = 40 cm

The distance of the point B from the point O = OB = 20 cm

(i) Whereby the point A is on the left of the meter rule, and taking the mass of half the meter rule as acting on the center, of the midspan from the left edge to the center, O, which is the point, D we have;

The total anticlockwise moment, Mₐ = 150 × 40 + 50 × OD = 6000 + 50 × OD

(ii) The total clockwise moment about O, is given similarly as follows;

The total clockwise moment,
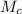`M_c` = 250 × 20 + 50 × OC = 5000 + 50 × OC

(iii) The difference between the anticlockwise and the clockwise moment = Mₐ -
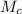`M_c` = 6000 + 50 × OD - 5000 + 50 × OC

Where, OD = OC, we have;

Mₐ -
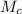`M_c` = 6000 + 50 × OD - 5000 + 50 × OD = 1,000

Mₐ -
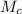`M_c` = 1000 N·cm

Therefore, Mₐ >
`M_c`

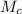
(iv) The distance from O where a 100 g force should be placed to balance the meter rule should give a 1000 N·cm clockwise moment as follows;

Let the 100 gf load be placed at the point E, to the right of the point O, therefore;

100 gf × OE = 1000 N·cm

OE = 1000/(100) = 10

OE = 10 cm

Therefore, the 100 gf should be placed 10 cm to the right of the point O.