Question

13. When the cost of fuel rose by 10%, Albert decreased his fuel consumption by 10%. Albert claimed that there was no change in his expenditure on fuel consumption. Explain if Albert is right or wrong.​

Answer 1

Wrong

Explanation:

Let cost of Albert's fuel be x.

When cost of fuel rises by 10% :

• x (1 + 10%)
• x (1 + 0.1)
• 1.1x

When consumption is reduced by 10% :

• 1.1x (1 - 10%)
• 1.1x (1 - 0.1)
• 1.1x (0.9)
• 0.99x

So clearly there is a 1% change in expenditure. Hence, Albert's claim is wrong.

Answer 2

Albert is wrong -- explanation below

Explanation:

Albert's expenditure "C" on fuel at any point in time is the product of the unit price, "p", and the amount of fuel purchased, "n".

In an equation form,
`C=pn`.

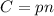Looking at some time before the changes, let's denote the unit price, the amount of fuel, and the expenditure with subscripts "1" to denote specific values at time 1, before the changes.

`C_1 = p_1 n_1`

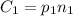
After the changes, note that p1 increased by 10%, and amount of fuel decreased by 10%.

Understanding changing percentages

For values that stay the same, we would multiply by 100% (or 1.00), since multiplying by 1 doesn't change the value.

For a 10% increase, we need 100%+10% which equals 110% or 1.10

For a 10% decrease, we need 100%-10% which equals 90% or 0.90

So, the new prices and amounts and costs at some later time, time 2, are given by
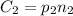`C_2 = p_2 n_2`, where
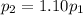`p_2 = 1.10p_1` and
`n_2 = 0.90n_1`.

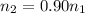Substituting:

`C_2 = p_2 n_2`

`C_2 = (1.10p_1) (0.90n_1)`

`C_2 = 0.99 p_1 n_1`

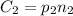
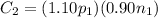
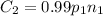
But remember that
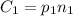`C_1 = p_1 n_1`, so

`C_2 = 0.99 C_1`

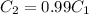
In other words, the next expenditure is 99% as much as (or 1% less than) the old expenditure.

Thus, Albert is incorrect to state that there was NO change in his expenditure.