Given:
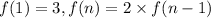 ...(i)
...(i)
For
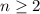 .
.
To find:
The nth term for the given recursive formula.
Solution:
The given recursive formula is of the form of
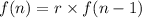 ...(ii)
...(ii)
It is the recursive formula of a GP, where r is common ratio.
On comparing (i) and (ii), we get
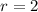
Now,
First term:
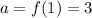
Common difference:
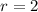
nth term of a GP is
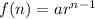
Putting a=3 and r=2, we get
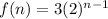
Therefore, the equation for the nth term is
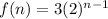 .
.