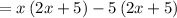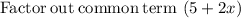Answer:
Please check the explanation.
Explanation:
4)
If an equation representing a parabola is in vertex form such as
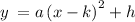
then its vertex will be at (k, h).
Therefore the equation for a parabola with a vertex at (-1, 3), will have the general form

If this parabola also passes through the point (1, -5) then we can determine the 'a ' parameter.
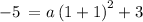
simplifying the equation
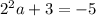

subtract 3 from both sides

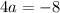
Divide both sides by 4
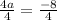
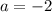
So our equation in vertex form is:
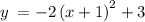
5)
Given the expression
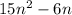
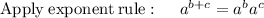
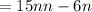

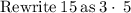
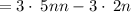
Factor out the common term 3n

6)
Given the expression
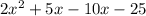
Factor 2x²+5x: x(2x+5)
Factor -10x-25: -5(2x+5)
so the expression becomes