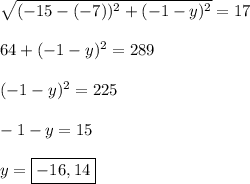Question

5

сл
Type the correct answer in each box.
A circle is centered at the point (-7, -1) and passes through the point (8, 7).
The radius of the circle is
units. The point (-15,
) lies on this circle.

Answer 1

Part 1: Finding radius

The radius of a circle is defined as the distance from the center to a point on the circle's circumference.

Using the distance formula,

`r=\sqrt{(-7-8)^(2)+(-1-7)^(2)}=\boxed{17}`

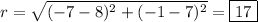
Part 2: Finding the point with x-coordinate -15

Let the y coordinate of the point be y. Then, we have the point (-15, y). Substituting into the distance formula,

`\sqrt{(-15-(-7))^(2)+(-1-y)^(2)}=17\\\\64+(-1-y)^(2)=289\\\\(-1-y)^(2)=225\\\\-1-y =\om 15\\\\y=\boxed{-16, 14}`