Question

Identify the following series as arithmetic, geometric, both, or neither


`2x + 2 {x}^(2) + 2 {x}^(3) + ... + 2 {x}^(n)`
​

Answer 1

Given:

The series is

`2x+2x^2+2x^3+...+2x^n`

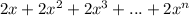
To find:

Whether the given series is arithmetic, geometric, both, or neither.

Solution:

We have,

`2x+2x^2+2x^3+...+2x^n`

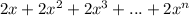
Difference between consecutive terms are:

`d_1=a_2-a_1`

`d_1=2x^2-2x`

`d_1=2x(x-1)`

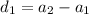
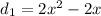
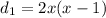
And,

`d_2=a_3-a_2`

`d_2=2x^3-2x^2`

`d_2=2x^2(x-1)`

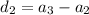
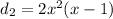
Here,
`d_1\\eq d_2`.

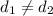So, the given series is not an arithmetic series.

Ratio between consecutive terms are:

`r_1=(a_2)/(a_1)`

`r_1=(2x^2)/(2x)`

`r_1=x`

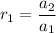
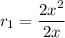
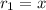
And,

`r_2=(a_3)/(a_2)`

`r_2=(2x^3)/(2x^2)`

`r_2=x`

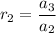
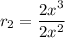
Similarly upto last pair of consecutive terms.

`r_(n-1)=(a_n)/(a_(n-1))`

`r_(n-1)=(2x^n)/(2x^(n-1))`

`r_(n-1)=x`

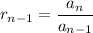
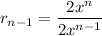
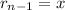
Since,
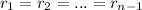`r_1=r_2=...=r_(n-1)`, so the given series have a common ratio.

Therefore, it is a geometric series.