Answer:
The passenger aircraft would take 10.542 years to reach the Sun from the Earth.
The passenger aircraft would take
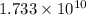 years to reach the gallactic center.
years to reach the gallactic center.
Step-by-step explanation:
The distance to the sun from the Earth is approximately equal to
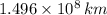 , if the passenger travels at constant speed, then the time needed to reach the sun is calculated by the following kinematic formula:
, if the passenger travels at constant speed, then the time needed to reach the sun is calculated by the following kinematic formula:
 (1)
(1)
Where:
 - Travelled distance, measured in kilometers.
- Travelled distance, measured in kilometers.
 - Speed of the passenger aircraft, measured in kilometers per second.
- Speed of the passenger aircraft, measured in kilometers per second.
 - Travelling time, measured in seconds.
- Travelling time, measured in seconds.
If we know that
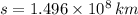 and
and
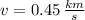 , then the travelling time is:
, then the travelling time is:

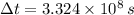


The passenger aircraft would take 10.542 years to reach the Sun from the Earth.
The distance between the Earth and the galactic center is approximately equal to
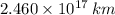 . If the passenger travels at constant speed and if we know that
. If the passenger travels at constant speed and if we know that
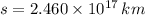 and
and
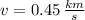 , then the travelling time is:
, then the travelling time is:
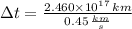
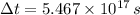
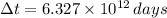
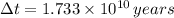
The passenger aircraft would take
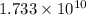 years to reach the gallactic center.
years to reach the gallactic center.