Question

Use a matrix to solve the system:

Answer 1

(2.83 , 1 , 4)

Explanation:

`2x+2y-z=4\\4x-2y-2z=2\\3x+3y-4z=-4\\`

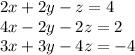
Rewrite these equations in matrix form

`\left[\begin{array}{ccc}2&2&-1\\4&-2&-2\\3&3&-4\end{array}\right] \left[\begin{array}{ccc}x\\y\\z\end{array}\right]=\left[\begin{array}{ccc}4\\2\\-4\end{array}\right] \\`

we can write it like this,

`AX=B\\X=A^(-1)B`

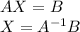
so to solve it we need to take the inverse of the 3 x 3 matrix A then multiply it by B.

We get the inverse of matrix A,

`A^(-1)=\left[\begin{array}{ccc}7/15&1/6&-1/5\\1/3&-1/6&0\\3/5&0&-2/5\end{array}\right] \\`

now multiply the matrix with B

`X=A^(-1)B\\\\\left[\begin{array}{ccc}x\\y\\z\end{array}\right] =\left[\begin{array}{ccc}7/15&1/6&-1/5\\1/3&-1/6&0\\3/5&0&-2/5\end{array}\right]\left[\begin{array}{ccc}4\\2\\-4\end{array}\right] \\\\\\\left[\begin{array}{ccc}x\\y\\z\end{array}\right] =\left[\begin{array}{ccc}2.83\\1\\4\end{array}\right] \\`