Question

Math Club members are selling games and puzzles. They make a profit of $10 per game and $8 per puzzle. They would like to make a profit of at least $200.

Answer 1

a)
`10x+8y \geq 200`

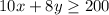
b) The members should sell at least 15 puzzles

Explanation:

Let x represents selling games

and y represents puzzles

The statement given is: They make a profit of $10 per game and $8 per puzzle. They would like to make a profit of at least $200.

a) The inequality will be:

`10x+8y \geq 200`

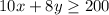
at least 200 means the profit can be equal to 200 or greater than that.

b) If the members sell 8 games, how many puzzles would they have to sell?

Number of puzzles sold can be solved by solving the inequality
`10x+8y \geq 200`

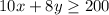
Put x =8 and find value of y

`10x+8y \geq 200\\10(8)+8y\geq 200\\80+8y\geq 200\\8y\geq 200-80\\8y\geq 120\\y\geq (120)/(8)\\y\geq 15`

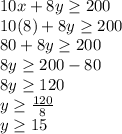
So, the members should sell at least 15 puzzles to make the inequality true. because the profit should be at least $200.