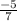Question

What is the slope of the line NP

Answer 1

The slope of NP is
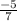`(-5)/(7)` ⇒ B

Explanation:

• In any square, every two opposite sides are parallel and every two consecutive sides are perpendicular

• Parallel lines have the same slope

• The product of the slopes of the perpendicular lines is -1, which means if the slope of one m, then the slope of the other is
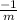  `(-1)/(m)` (reciprocal m and change its sign)

• The rule of the slope of the line which passes through the points (x1, y1) and (x2, y2) is m =
  `(y2-y1)/(x2-x1)`

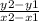
In square MNPR

∵ MN and NP are adjacent sides

∴ MN ⊥ NP

∵ M = (3, 8) and N = (-2, 1)

∴ x1 = 3 and y1 = 8

∴ x2 = -2 and y2 = 1

→ Use the rule of the slope above to find the slope of MN

∴ m(MN) =
`(1-8)/(-2-3)`

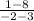
∴ m(MN) =
`(-7)/(-5)`

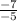
∴ m(MN) =
`(7)/(5)`

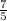
∵ MN ⊥ NP

∴ The product of their slopes = -1

→ Reciprocal the slope of MN and change its sign

∴ m(NP) =
`(-5)/(7)`

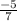
∴ The slope of NP is
`(-5)/(7)`