Answer:
Explanation:
Alright we need to prove that both the triangles are similar so lets get started
The slope formula is:
Slope = Change in y / Change in x
m = Δy / Δx
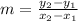
Where, m is the slope and
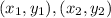 are any points on the line
are any points on the line
In this graph we are given three points which are
(0 , 2) , ( 6 , 6) and (9 , 8)
So for our first triangle we use the 2 points (0 , 2) and (6 ,6) and calculate the slope,
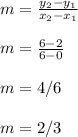
So the slope turns out to be 2/3 , Now for our second triangle use the 2 points (6 , 6) and (9 , 8)
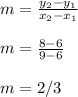
So we can see the the slope's are equal that's the answer to your first part.
Second part
Yes they are similar due to the property of corresponding angles where angle x of the first triangle equals angle x for the second triangle and angle y for the first triangle equals angle y for the second triangle and both the triangles have 90° se they are similar because all three angles are similar. (AAA = angle angle angle property) I have attached a to make you understand it better.