Question

An auditorium has 30 rows with 10 seats in the first row, 12 in the second row, 14 in the third row, and so forth. How many seats are in the auditorium? (1 point)

Answer 1

1170

Explanation:

hey there,

(the other person just calculated each number themselves then added them up which i guess is okay but not in the long term for when you're taking a test for example or your teacher asks you this kind of question so it's better to memorize a formula.)

< There are two types of sequences: arithmetic and geometric. So also two formulas for finding sums of each. This situation is an arithmetic sequence.

Formula for the sum of an arithmetic sequence:
`S_n=(n)/(2) (a_1+a_n)`

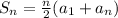
We know there are 30 total rows so n = 30. a1 is the very first term of a sequence so this is 10 in this situation. Before we fill in the formula, we should find what an is equal to.

For this, we will use the basic formula you learned previously:
`a_n=dn+c`

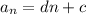
d (the common difference) = a2-a1 = 12-10=2

c (the common ratio) = a1-d = 10-2 = 8

an = dn + c = 2(30) + 8 = 68

Now that we have found what a_n is equal to, we can plug everything into the sum equation.

`S_n = (30)/(2) (10+68)=1170`

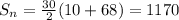
So 1170 is your final answer. >

Hope this helped! Feel free to ask anything else.

Answer 2

My answer is 1170 but the way I figured out the problem was by listing numbers 1-30. the problem state that the 1st row had 10, 2nd row had 12, and 3rd row had 14 and so forth. So I basically did the same method till I got to 30 and then add up all the numbers which gave me the answer of 1170.

Explanation: