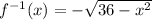Question

Find the inverse of “f” algebraically, please!

Answer 1

Answer:
`f^(-1)(x) = -√(36-x^2)`

====================================================

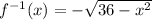
Here are the steps to find the inverse

`f(x) = √(36-x^2)\\\\y = √(36-x^2)\\\\x = √(36-y^2) \ \text{ swap x and y; solve for y}\\\\x^2 = 36-y^2\\\\x^2+y^2 = 36\\\\y^2 = 36-x^2\\\\y = √(36-x^2)\\\\f^(-1)(x) = √(36-x^2)\\\\`

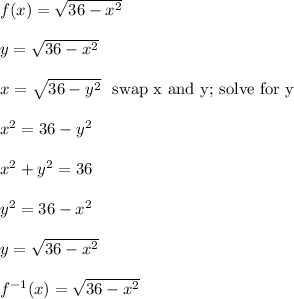
Now this would be the answer if our original domain was
`0 \le x \le 6`

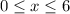
However, that's not the case and instead our domain is
`-6 \le x \le 0`

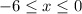
Reflecting any (x,y) point in this domain restriction, over the the line y = x, will have us land on a point with a negative y value. This is because the inverse will swap the x and y values.

Therefore, the inverse function must ultimately be negative.

Currently
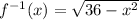`f^(-1)(x) = √(36-x^2)` is positive since the result of any square root is never negative.

To fix this, we stick a negative out front to get the final answer being
`f^(-1)(x) = -√(36-x^2)`