Answer:

Explanation:
This is a right triangle, which we know because of the little square in the corner.
We can use the Pythagorean Theorem:

where a and b are the legs and c is the hypotenuse.
In this triangle, 28 and 45 are the legs, because they make up the right angle. The unknown side is the hypotenuse, because it is opposite the right angle.
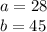
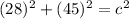
Solve the exponents.
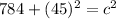
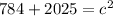
Add the two numbers.
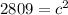
Solve for c by isolating it on one side of the equation. c is being squared. The Inverse of a square is the square root. Take the square root of both sides of the equation.
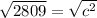
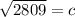

The third side and hypotenuse of the triangle is 53