Solve the equation: 5^x^(^x^-^1^)=1

Question

Solve the equation:
`5^x^(^x^-^1^)=1`

Answer 1

The concept:

We are given the equation:

`5^(x(x-1)) = 1`

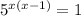
Which can be simplified as:

`5^{x^(2) - x} = 1^(1)`

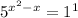
Since any number to the power '0' is 1

x² - x must be equal to 0 for the given equation to be true

Solving for x:

x² - x = 0

x(x-1) = 0

now, we can divide both sides by either x OR x-1

So we will see what we get for either choice:

x = 0/(x-1) x-1 = 0/x

x = 0 x = 1

Hence, the value of x is either 0 or 1