Question

Write an equation for a parabola in which the set of all points in the plane are equidistant from the focus and line F(-6,0); x=6

Answer 1

Explanation:

Since we have a vertical directrix, the equation of the parabola is

`(y - k) {}^(2) = 4p(x - h)`

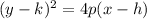
Where p is the distance from the vertex to the directrix.

or the distance from the vertex to the focus.

Since we have a sideways parabola, let use the point for the directrix is (-6,0). So let find the midpoint of (-6,0) and (6,0). That would be our vertex.

`( - 6 + 6))/(2) = 0`

`(0 + 0)/(2) = 0`

So our vertex is (0,0).

So our equation become

`{y}^(2) = 4px`

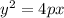
The distance from the focus and directrix is 6.

So p=6.

`{y}^(2) = 24x`

So p is 6.

Since p is 6,

`\frac{ {y}^(2) }{24} = x`