Question

How to write a paragraph proof for number 18?

Answer 1

See proof below

Explanation:

Triangle congruence

To prove triangles are congruent, we can go all the way back to the definition (never do this unless you have to), or we can use one of the triangle congruence theorems:

Prove triangle congruence by definition - prove all 3 corresponding angle pairs, and all 3 corresponding sides are congruent

Prove by Congruence theorem -

• SSS
• SAS
• ASA
• AAS, or
• HL

In this situation, the triangles aren't right triangles, so HL won't work.

We already have one angle congruent as a given, so we need two more parts: either another angle and any side, or else both sides adjacent to the angle.

Since the two triangles share a side, if we can get another angle (which it looks like you may have already identified, based on pencil markings on the diagram), we can prove triangle congruence.

General Outline

Accept givens

Prove
`\angle YTX \cong \angle TYS`

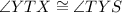
Prove/state shared side is congruent

Use AAS congruence

Proof

Accept
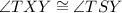`\angle TXY \cong \angle TSY` as given.

Given
`\overline {TX} || \overline{SY}`, observe that line TS contains point T, and line SY contains point Y, so line TY is a transversal to the pair of parallel lines TS and SY.

Since
`\angle YTX` and
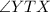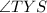`\angle TYS` are the alternate interior angles formed by a transversal across two parallel lines,
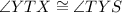`\angle YTX \cong \angle TYS` by the Alternate Interior Angles Theorem.

By the reflexive property of congruent line segments,
`TY \cong YT`.

Finally, given the pairs of corresponding parts already proven congruent, (two angles, and a side not contained by them), by AAS Triangle congruence,
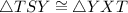`\triangle TSY \cong \triangle YXT`.